作为总结和回顾,本篇来梳理下开发和刷题过程中所遇到的常用数据结构。
首先什么是数据结构呢?在一般的算法书籍中都会告诉读者这句话:
$$程序 = 数据结构 + 算法$$
简单的来说,数据结构会描述数据的两个方面:
常用的数据结构有:
下面就来一一介绍
数组
定义
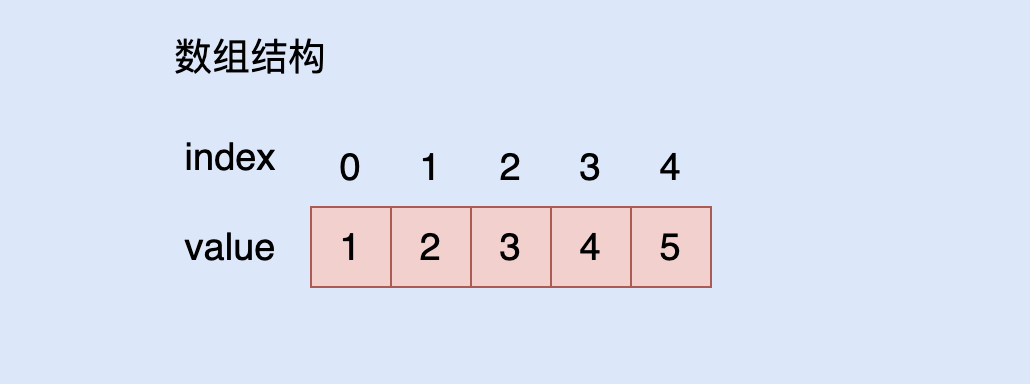
数组是由相同类型的数据组成的有限集合。它的特点是元素的类型相同,元素在内存中连续存储。

创建一个数组
1
2
3
|
func main() {
arr := []int{1,2,3,4,5}
}
|
操作
数组常用的操作有查询、插入和删除元素
查询元素
数组可以直接通过下标查询对应的元素,时间复杂度为 O(1)
1
2
3
4
|
func main() {
list := []int{1,2,3}
n := list[1]
}
|
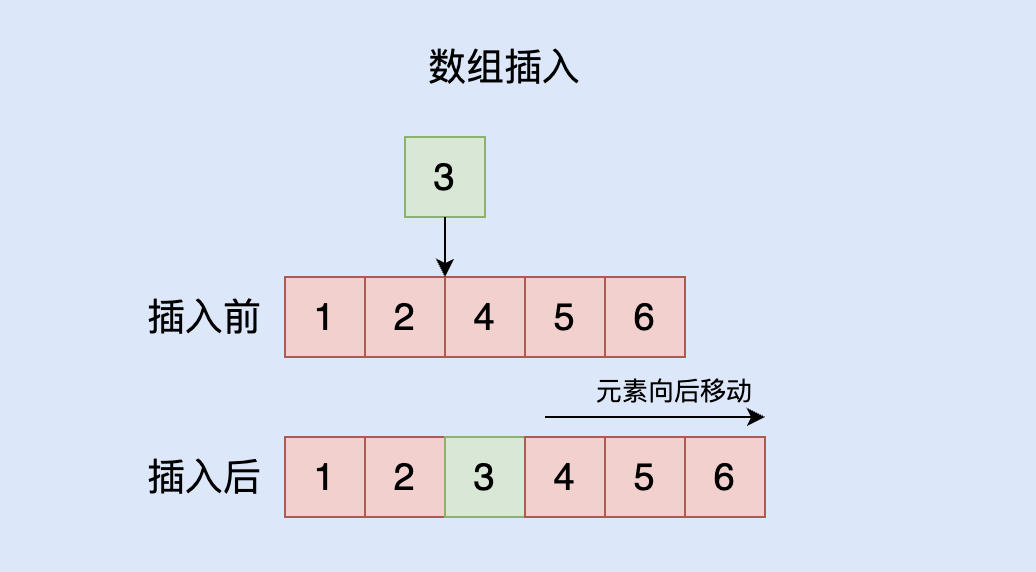
插入元素

插入元素的分成三个步骤:
- 查询下标
- 下标之后的元素向后放置
- 插入元素
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func Insert(list []int, index, n int) []int {
length := len(list)
// 检查边界
if index < 0 || index > length {
return list
}
// 数组扩展
list = append(list, n)
// 元素交换
for i := index; i <= length; i++ {
list[i], list[length] = list[length], list[i]
}
return list
}
|
当插入的位置为数组尾部时,时间复杂度为 O(1),其他情况则为 O(n)。平均状态下,数组插入的时间复杂度为 O(n)。
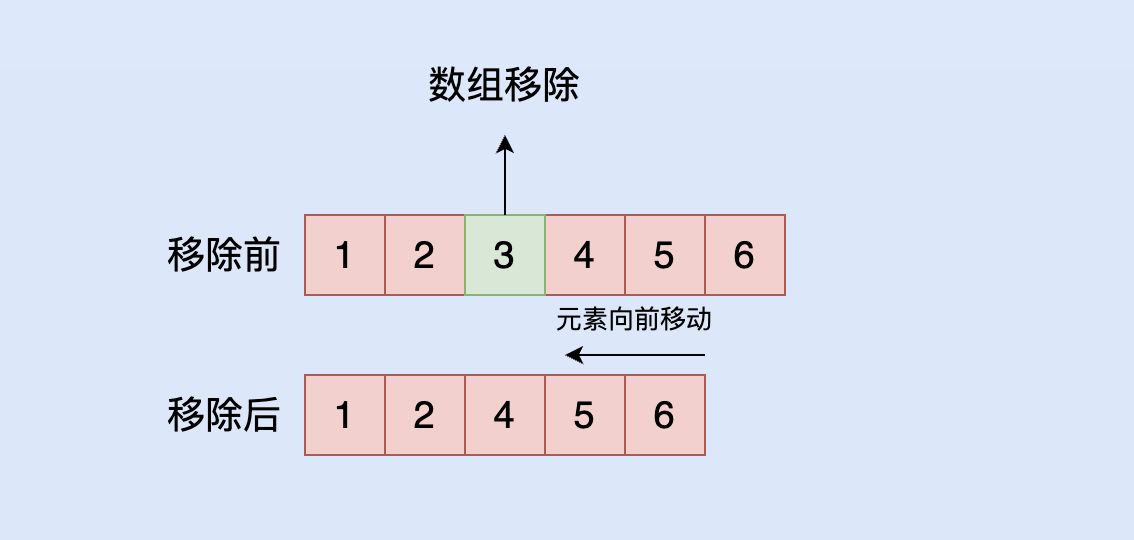
移除元素

移除元素的分成三个步骤:
- 查询下标
- 移除元素
- 下标之后的元素向前放置
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func Remove(list []int, index int) []int {
length := len(list)
if index < 0 || index >= length {
return list
}
// 元素交换
for i := index; i < length-1; i++ {
list[i] = list[i+1]
}
return list[:length-1]
}
|
当移除的位置为数组尾部时,时间复杂度为 O(1),其他情况则为 O(n)。平均状态下,数组移除的时间复杂度为 O(n)。
小结
数组是最简单的数据结构,它的特点是元素之间存储连续,查询元素高效。缺点是插入和删除时需要移动元素,容量变动时,需要申请新的连续内存空间,容易造成内存碎片。
链表
定义
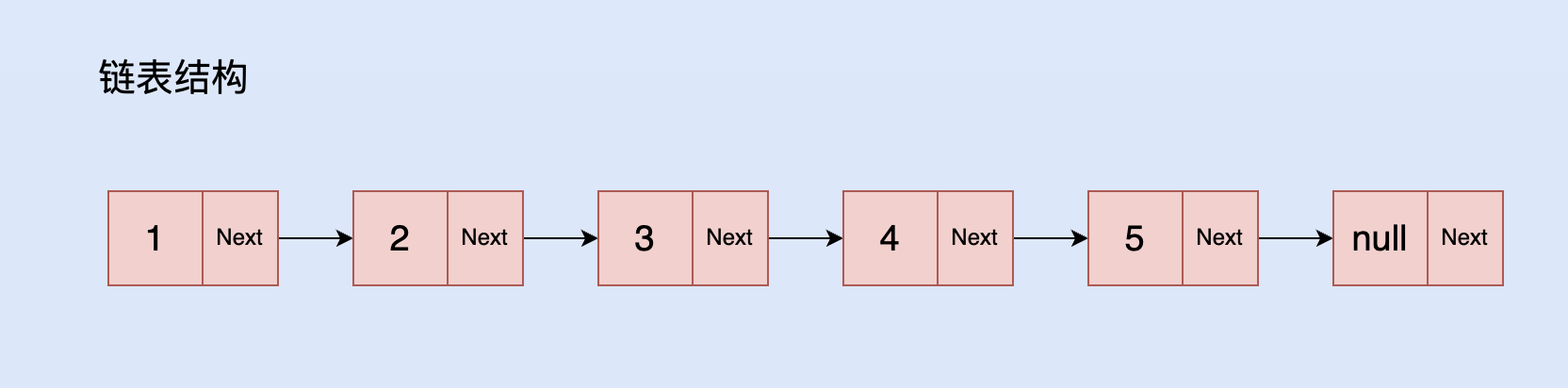
链表的定义和数组类似,但是它的每个元素除了值之外,还有一个指针域,指向下一个元素。链表中的元素称为节点。
1
2
3
4
|
type ListNode struct {
Val int
Next *ListNode
}
|

每个链表的节点由两个部分组成:数据域和指域。每个节点串联成一个列表。
操作
查询元素
链表的查询需要从第一个节点 head,依次遍历到对应的节点。所以查询操作的时间复杂度为 O(n)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func GetElement(head *ListNode, index int) *ListNode {
node := head
n := 0
for node != nil {
if n == index {
return node
}
n += 1
node = node.Next
}
return node
}
|
插入元素
链表的插入有以下步骤:
- 遍历找到对应的位置
- 创建新的节点
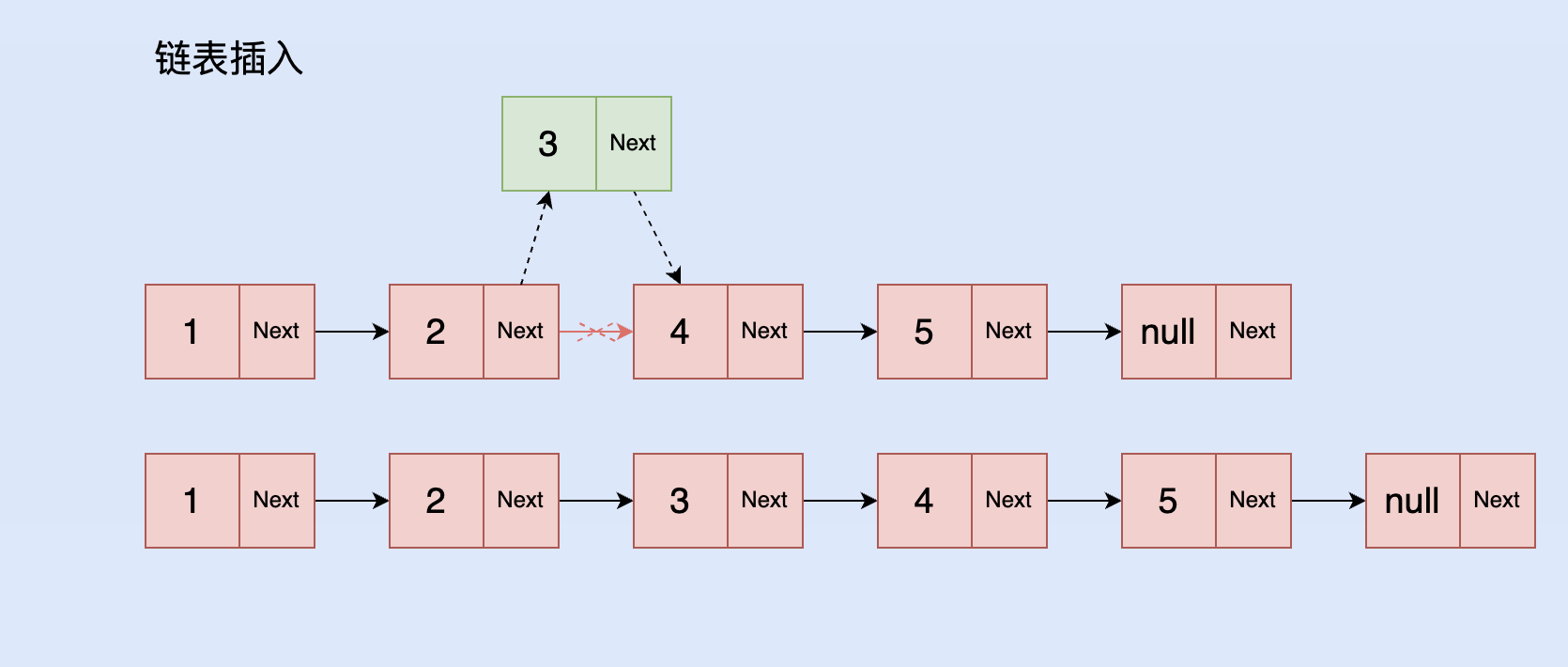
- 原节点的 Next 指向该节点,该节点的 Next 指向原节点的 Next。

插入时分三种情况说明:
- 头部插入时,插入节点的 Next 为 head,并修改 head 为插入的节点。
- 尾部插入时,尾部节点为插入节点,插入节点的 Next 为空。
- 中间插入时,效果如图所示。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func Insert(head *ListNode, index, val int) *ListNode {
if index == 0 {
head = &ListNode{Val: val, Next: head}
return head
}
n := 0
node := head
for node != nil {
// 定位到前一个节点
if n == index-1 {
node.Next = &ListNode{Val: val, Next: node.Next}
break
}
n += 1
node = node.Next
}
return head
}
|
链表插入的时间复杂度为 O(n)。
删除元素
链表的删除元素操作和插入类似:
- 定位节点
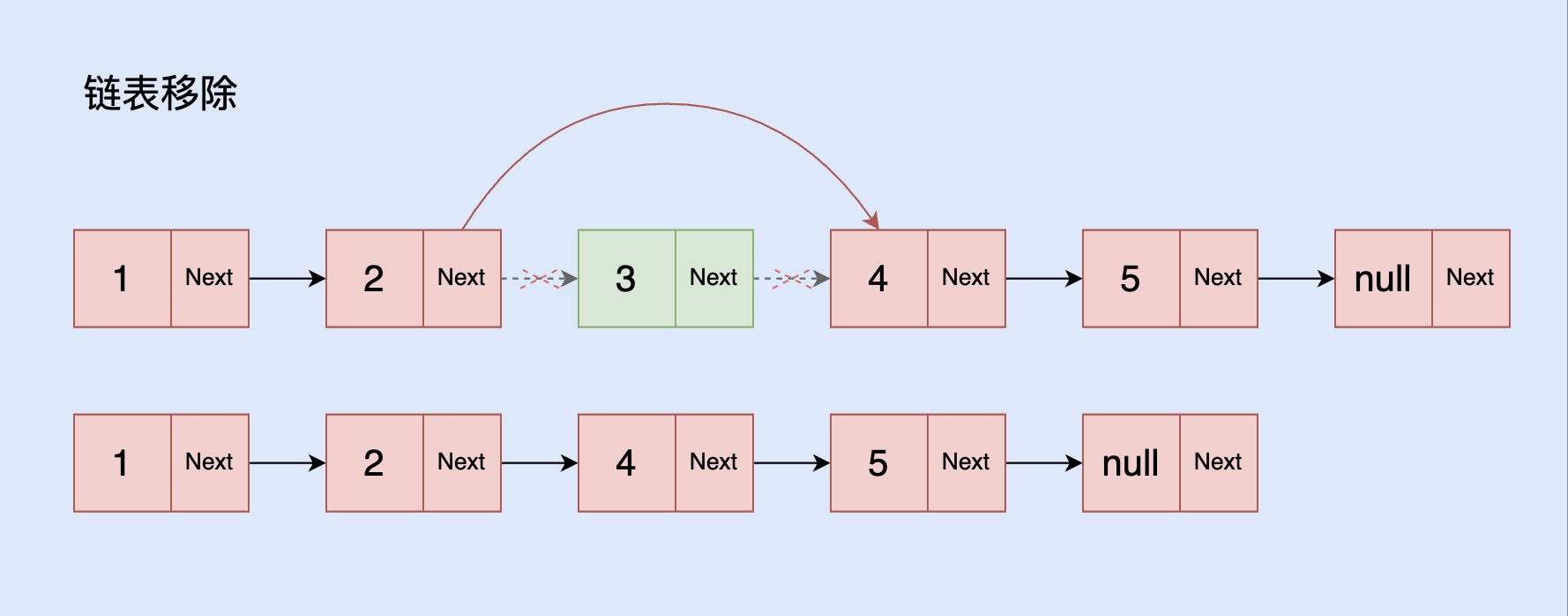
- 待移除的前一个节点的 next 指向带移除节点的 next
- 移除节点

移除时分三种情况说明:
- 头部移除时,head 变成 head.Next
- 尾部移除时,尾部变成空节点
- 中间移除时,效果如图所示。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func DeleteNode(head *ListNode, val int) *ListNode {
fast := head
var slow *ListNode
for fast != nil {
if fast.Val == val {
if slow == nil {
head = fast.Next
} else {
slow.Next = fast.Next
}
break
}
slow = fast
fast = fast.Next
}
return head
}
|
其他链表结构
在链表结构在单链表的基础上还衍生出其他的变种,如循环链表、双链表。
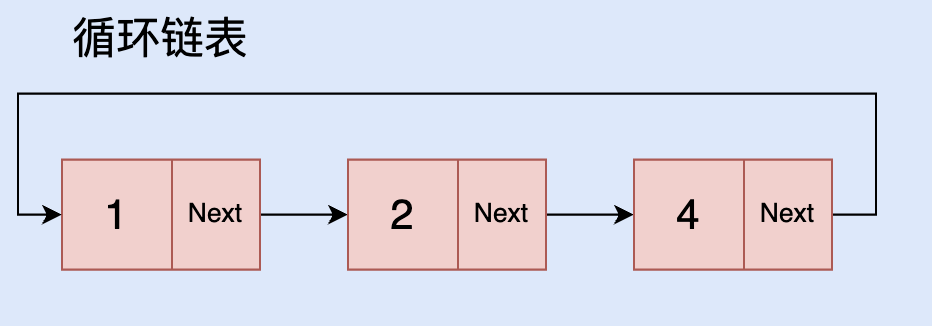
循环链表
 循环链表的尾指针指向头节点,它可以将尾部插入和删除的时间节点优化为 O(1)。
循环链表的尾指针指向头节点,它可以将尾部插入和删除的时间节点优化为 O(1)。
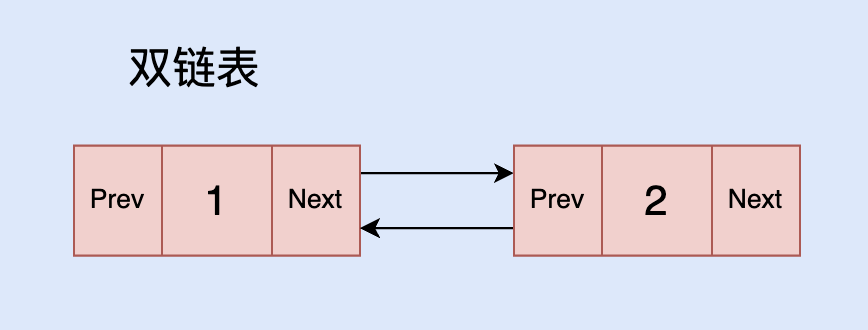
双连链表

双链表的每个节点有一个额外的 Prev 指针指向上一个节点,它可以优化链表的反向遍历。但是因为多一个指针域,所以插入和删除节点时的操作更加复杂。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
type DoubleNode struct {
Val int
Prev *DoubleNode
Next *DoubleNode
}
func DoubleNodeInsert(node *DoubleNode, val int) {
// ...
next := node.Next
cur := &DoubleNode{Val: val}
cur.Next = next
cur.Prev = node
next.Prev = node
node.Next = cur
// ...
}
func DoubleNodeRemove(node *DoubleNode) {
// ...
prior := node.Prev
next := node.Next
prior.Next = next
next.Prev = prior
// ...
node = nil
}
|
它们本质上都是一种以空间换时间的优化方式。
小结
链表和数组都是线性表,元素的类型相同,且元素之间顺序存放。它们是最基本数据结构,在此基础上可以构建出其他更复杂的数据结构。虽然数据和链表在定义和功能上相似,但是它们也各有特点:
| 数据结构 |
存储分配方式 |
时间性能 |
空间性能 |
| 数组 |
在内存中用一段连续的存储单元依次存储数据元素 |
查找为 O(1), 插入和删除在(需要移动后续元素)为 O(1) |
需要预分配存储空间,容易造成内存碎片。当需要的数组容量过大时可以没有足够的空间可以申请。 |
| 链表 |
采用链式存储结构,用一组任意的存储单元存放数据元素 |
查找为 O(n), 查找和删除为 O(n),但是不需要移动元素,性能优于数组 |
不需要预分配,元素个数也不受限制,因为多一个指针域,所以每个节点所占用的空间大于数组 |
队列
定义
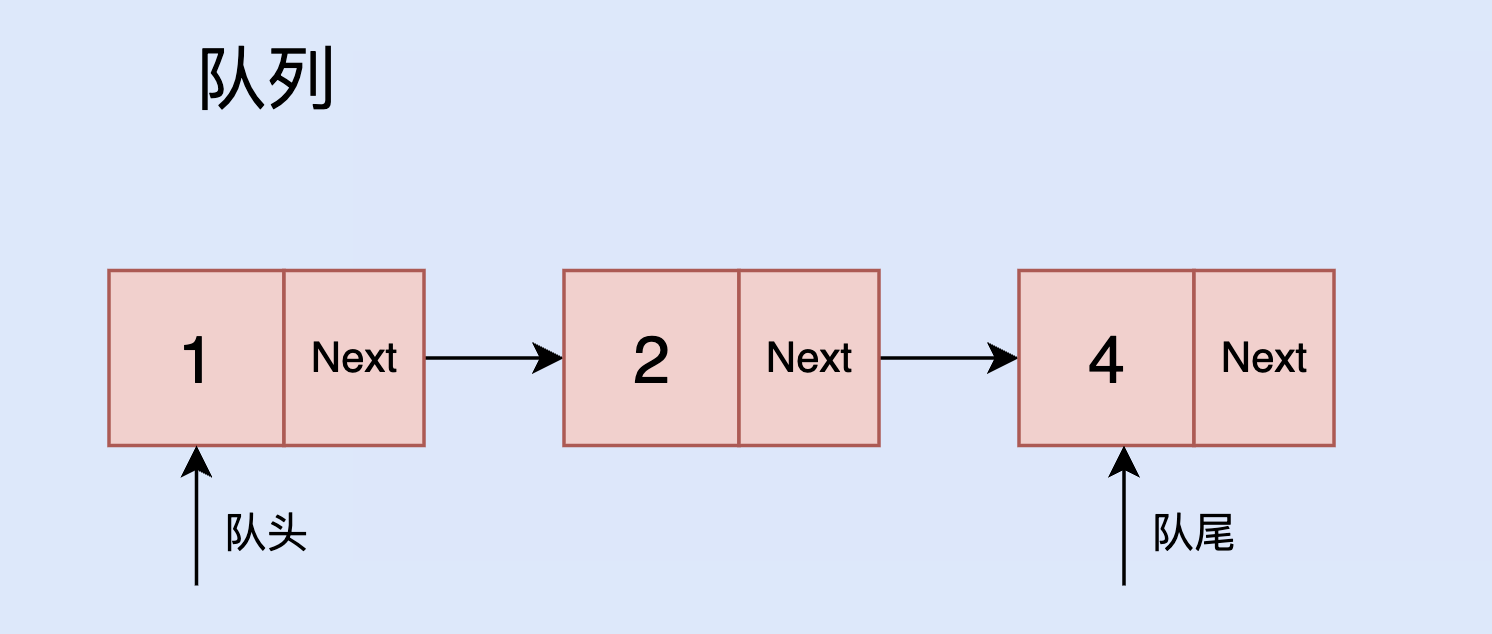
队列是一种先进先出 (FIFO) 的线性表。队列有队头和队尾,元素从队尾添加,从队头取出。
队列的实现方式有多种,可以使用数组或是链表来实现。实际上,只要能保证 FIFO,队列内部如何实现都不重要。

1
2
3
4
5
6
7
8
9
10
11
12
13
|
type Node struct {
Val int
Next *Node
}
type Queue struct {
head *Node
tail *Node
}
func NewQueue() *Queue {
return &Queue{}
}
|
操作
队列主要的操作为 push (入队) 和 pop (出队)。
push 入队
直接从队列的尾部直接追加新的元素,需要注意的是,如果队列为空,队列的头尾指针要同时指向新的元素。如果不为空,追加元素后需要更新队尾指针指向新的元素。
1
2
3
4
5
6
7
8
9
10
|
func (q *Queue) Push(val int) {
node := &Node{Val: val}
if q.head == nil {
q.head = node
q.tail = node
return
}
q.tail.Next = node
q.tail = node
}
|
入队的时间复杂度为 O(1)。
pop 出队
在队列不为空时,直接输出队头元素的值并更新队头指针指向后一个元素。
1
2
3
4
5
6
7
8
|
func (q *Queue) Pop() (int, error) {
if q.head == nil {
return 0, fmt.Errorf("empty queue")
}
val := q.head.Val
q.head = q.head.Next
return val, nil
}
|
出队的时间复杂度为 O(1)。
优先队列
优先队列是一种特殊队列,队列中的每一个元素带有权重值。这时队列不再是简单的 FIFO,而且权重值高的元素优先出队。优先队列内部使用二叉堆实现。
小结
队列具有先进先出的特点,它常见的操作有入队 (Push) 和出队 (Pop),时间复杂度为 O(1)。总的来说,队列是一种简单的数据结构,常见的使用场景是处理具有先后顺序的任务。
栈
定义
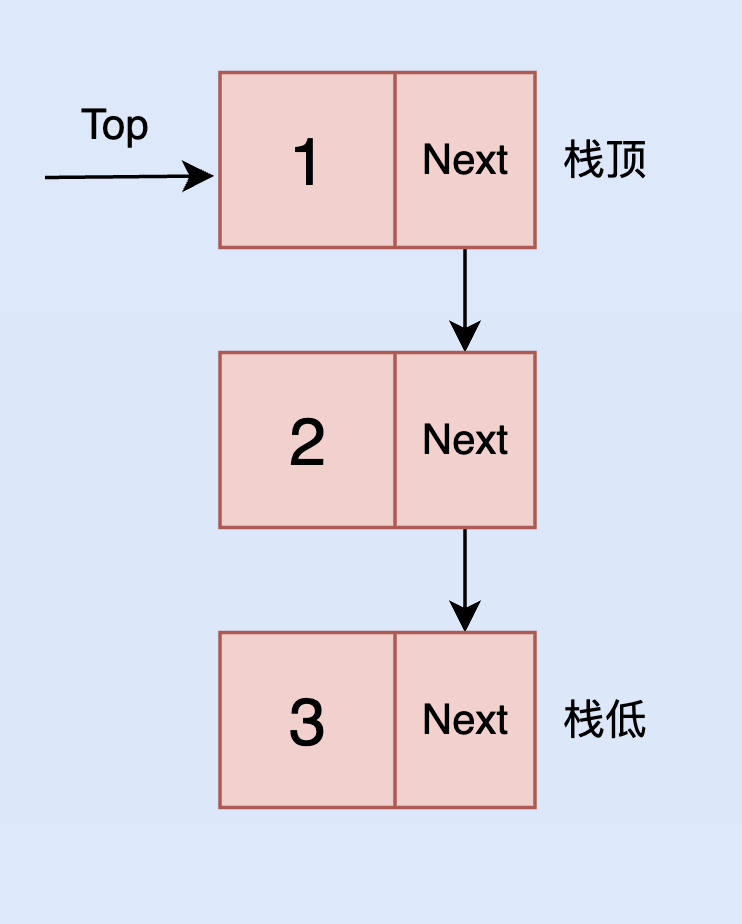
栈和队列相反,它是一种具有先进后出的线性表。元素从栈顶添加,从栈顶移除。我们可将栈想像成一个存放小球的圆筒,桶的宽度只能容纳一个小球。每次放入小球时,先进的球就会落到底部,而每次从桶中取出是,总是从桶的顶部开始。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
type Node struct {
Val int
Next *Node
}
type Stack struct {
top *Node
}
func NewStack() *Stack {
return &Stack{}
}
func (s Stack) String() string {
out := make([]string, 0)
p := s.top
for p != nil {
out = append(out, strconv.Itoa(p.Val))
p = p.Next
}
return strings.Join(out, "->")
}
|
操作
栈的常见操作为 Push(进栈) 和 Pop (出栈)。
Push 进栈
从栈顶添加一个新的元素,新元素的 Next 指针指向 top 节点,并更新 top 指针指向新的元素。
1
2
3
4
5
6
7
8
9
|
func (s *Stack) Push(val int) {
node := &Node{Val: val}
if s.top == nil {
s.top = node
return
}
node.Next = s.top
s.top = node
}
|
进栈操作的时间复杂度为 O(1)。
Pop 出栈
在栈不为空情况下,取出 top 元素的值,并更新 top 指针指向指向到下一个节点。
1
2
3
4
5
6
7
8
|
func (s *Stack) Pop() (int, error) {
if s.top == nil {
return 0, fmt.Errorf("empty stack")
}
val := s.top.Val
s.top = s.top.Next
return val, nil
}
|
小结
栈和队列结构相似,只是在操作上的处理有写不同。栈操作的时间复杂度都是 O(1)。栈也支持使用数组和链表的方式实现。如果栈的容量小,使用数组更有优势,反之则选链表。
字符串
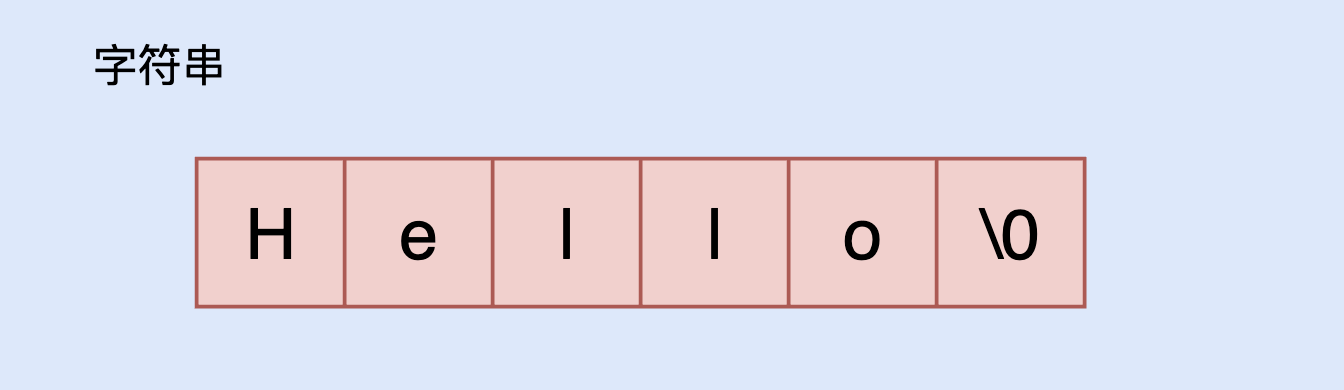
字符串是由零个或多个字符组成的有限序列。

字符串常见的操作为模式匹配。模式匹配算法有: KMP、BM 和 BF 算法。
哈希表
定义
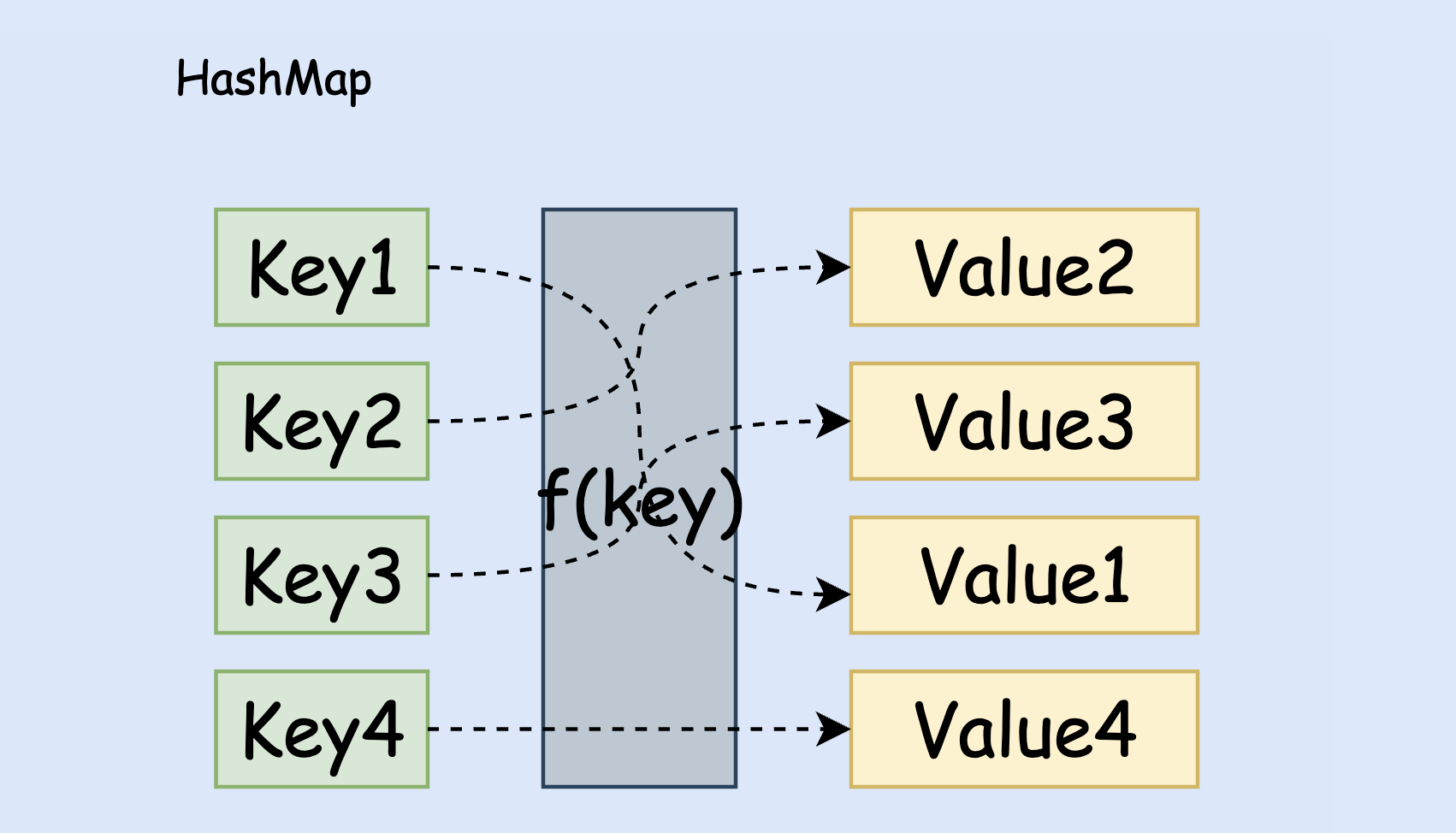
哈希表也叫散列表,是一种使用散列函数 f(key) 建立关键字 (key) 与具体值 (value) 对应关系的数据结构。哈希表的值一般存储在数组中。
哈希表的读写性能优异,平均时间复杂度为 O(1)。哈希表性能优异的关键点在于哈希函数和解决哈希冲突。

哈希函数
哈希表的哈希函数有:
最为常见的是除留取余法。对于散列表长为 m 的散列函数公式为:
$$
f(key) = key \ mod \ p \ (p \leq m)
$$
根据经验,若哈希表表长为 m,通常 p 为小于或者等于表长 (最好接近 m) 的最小质数或不包含小于 20 质因子的合数。
哈希冲突
在理想状态下,每个 key 经过哈希函数后都有一个唯一值。但是理想丰满,现实骨感。没有完美哈希函数,当哈希表的容量不断扩大时,不可避免的会出现哈希冲突 (不同 key 经过哈希函数后指向相同的哈希地址)。出现冲突后哈希表的性能会急剧下降,极端情况下会变成 O(n)。
既然冲突不可避免,那如何处理冲突就成为关键点。解决哈希冲突的方式有:
- 开放寻址法:如果发生冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到。
- 再哈希法:如果发生冲突,就换一张散列函数,直到冲突解决。
- 公共溢出区法:建立一个公共的溢出区,冲突的关键字将存放在此处。
- 链地址法:哈希表的存储结构变成数据加上链表。每个关键字对应存储地址变成单链表的头指针。有时为了预防极端情况出现,会用红黑树代替单链表。
装载因子
$$
装载因子 = 哈希表元素 / 长度
$$
随着装载因子的增加,线性探测的平均用时就会逐渐增加,这会影响哈希表的读写性能。当装载率超过 70% 之后,哈希表的性能就会急剧下降,而一旦装载率达到 100%,整个哈希表就会完全失效,这时查找和插入任意元素的时间复杂度都是 𝑂(n) 的,这时需要遍历数组中的全部元素,所以在实现哈希表时一定要关注装载因子的变化。
而为了保证哈希表的性能,这个时候就会考虑对哈希表扩容。
小结
总的来说哈希表是一种常用高性能数据结构。在查找算法中具有很大用途。但是想要维持它的高性能就需要处理好哈希冲突问题。
树
树是一种较复杂的数据结构。
定义
树 (Tree) 是 n $ (n \geq 0) $ 个节点的有限集合

树有很多相关的概念:
- 根结点 (root):树的最顶端结点被称为树的根结点。每棵树都有一个根结点,它是树的入口。
- 子树 (SubTree):非根结点的每个集合本身又是一棵树,它们是根的子树。
- 度 (Degree):结点拥有的子树数称为结点的度。
- 叶结点 (Leaf):度为 0 的结点称为叶结点。
- 树的深度 (Depth):根结点到叶结点的最大层数称为树的深度。
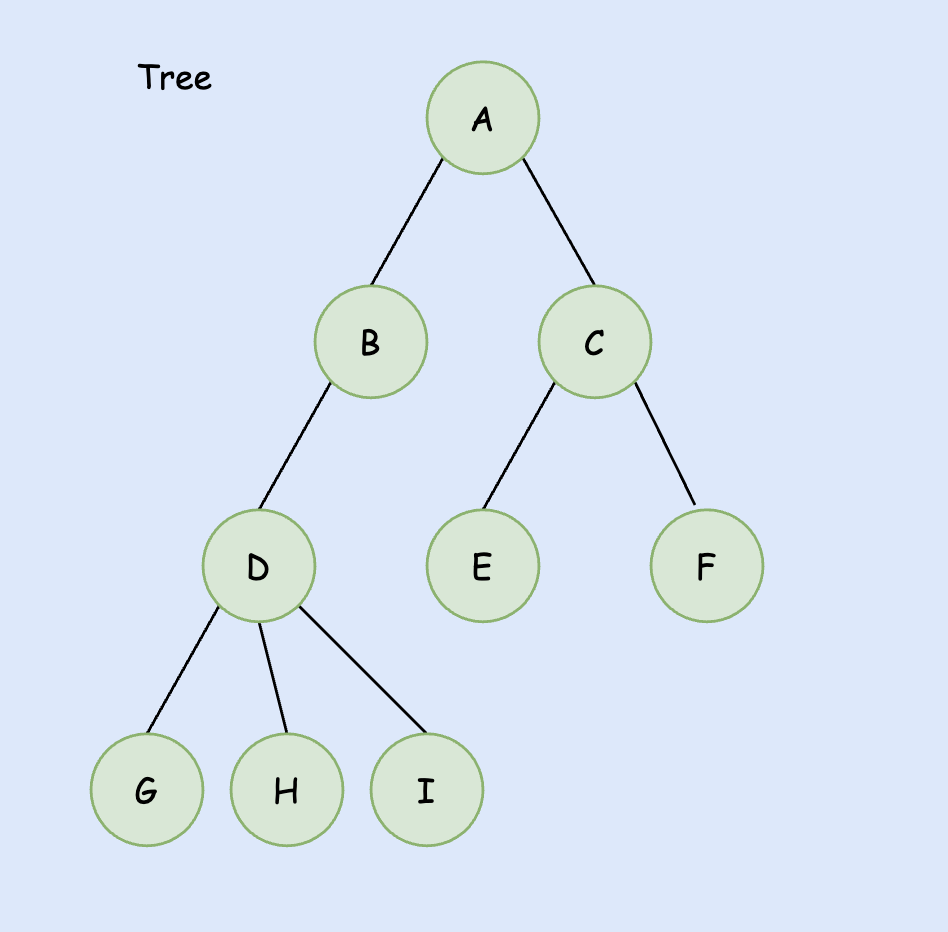
二叉树
二叉树的每个结点最多只有两棵子树,分别为左子树和右子树。
树结点
1
2
3
4
5
|
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
|
特殊的二叉树
1. 满二叉树
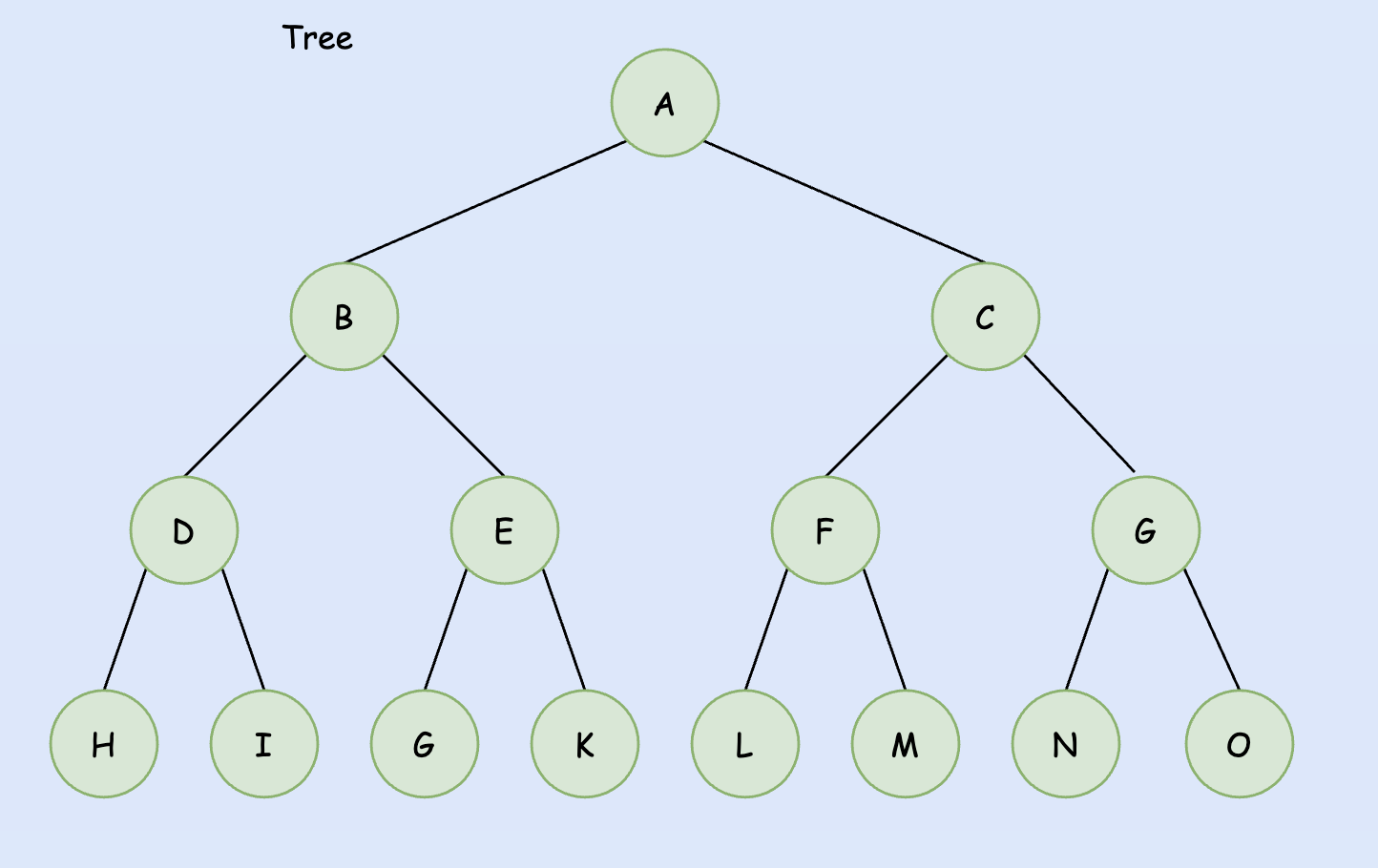
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子树都在同一层上,这样的二叉树称为满二叉树。

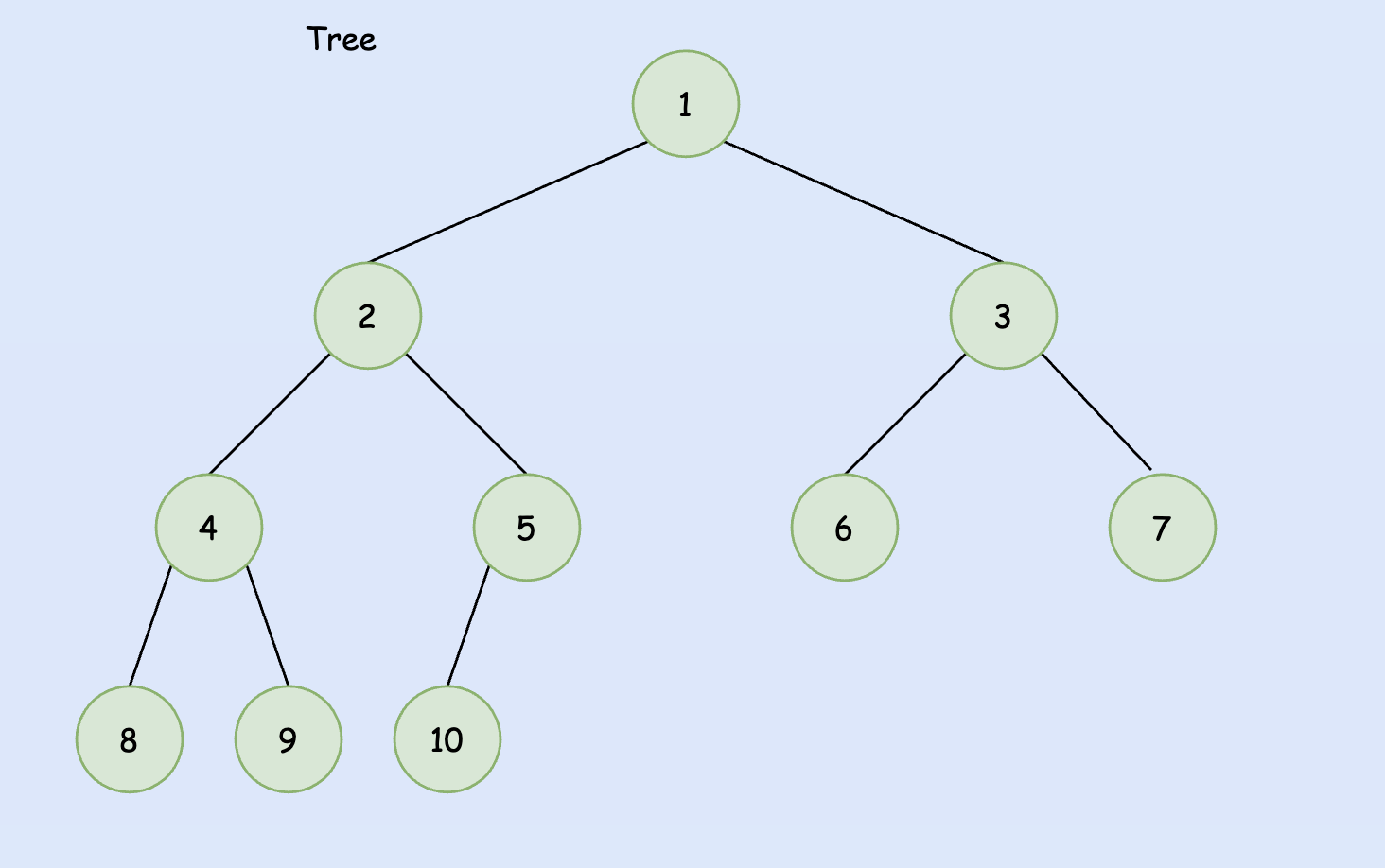
2. 完全二叉树
对一棵具有 n 个结点的二叉树按层序编号,如果编号为 i $(i \leq i \leq n)$ 的结点与同样深度的满二叉树中编号为 i 的节点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。

如何判断一棵树是否是完全二叉树? 可以对照树的示意图,给每个结点按照满二叉树的结构逐层顺序编号,如果编号出现空档,就说明不是完全二叉树,反之则是。
二叉树的性质
性质1: 在二叉树的第 i 层上至多有 $2^{i-1}$ 个节点 $ ( i \geq 1) $。
性质2: 深度为 k 的二叉树至多有 $2^k-1$ 个节点 $(k \geq 1)$。
性质3: 对任何一棵二叉树 T,如果其叶结点数为 $n_0$,度为 2 的结点数为 $n_2$,则 $ n_0 = n_2 + 1$ 。
性质4: 具有 n 个结点的完全二叉树的深度为 $[log_2n]+1$ ($[x]$ 表示不大于 x 的最大整数)。
性质5: 如果对一个有 n 个结点的完全二叉树 (其深度为$[log_2n]+1$) 的节点按层序编号 (从第1层到第$[log_2n]+1$层,每层从左到右),对任一结点 i ($i \leq i \leq n$) 有:
- 如果 $i=1$,则结点 i 是二叉树的根,无双亲;如果 $i > 1$,则其双亲是节点 $[i/2]$ 。
- 如果 $2i>n$,则结点 i 无左孩子 (结点 i 为叶子结点);否则其左孩子是结点 2i。
- 如果 $2i+1>n$,则结点 i 无右孩子;否则其右孩子是结点 2i+1 。
二叉树的遍历
二叉树的遍历 (traversing binary tree) 是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且被访问一次。
二叉树存在四种遍历方式:前序、中序、后序和层序。
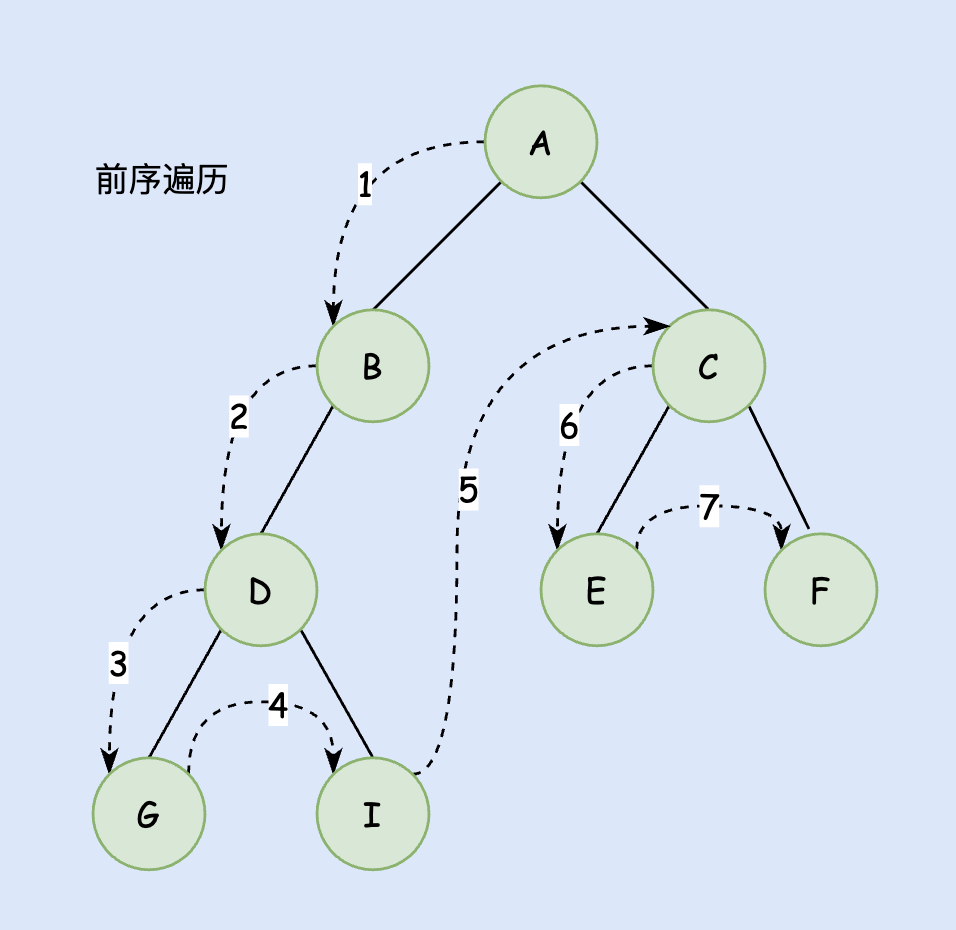
前序遍历

前序遍历的循序的: Val -> Left -> Right
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
// 递归方式
func PreorderTraversal1(root *TreeNode) []int {
out := make([]int, 0)
var traversal func(*TreeNode, *[]int)
traversal = func(root *TreeNode, out *[]int) {
*out = append(*out, root.Val)
traversal(root.Left, out)
traversal(root.Right, out)
}
traversal(root, &out)
return out
}
// 迭代方式
func PreorderTraversal2(root *TreeNode) []int {
vals := make([]int, 0)
stack := make([]*TreeNode, 0)
node := root
for node != nil || len(stack) > 0 {
for node != nil {
vals = append(vals, node.Val)
stack = append(stack, node)
node = node.Left
}
node = stack[len(stack)-1].Right
stack = stack[:len(stack)-1]
}
return vals
}
|
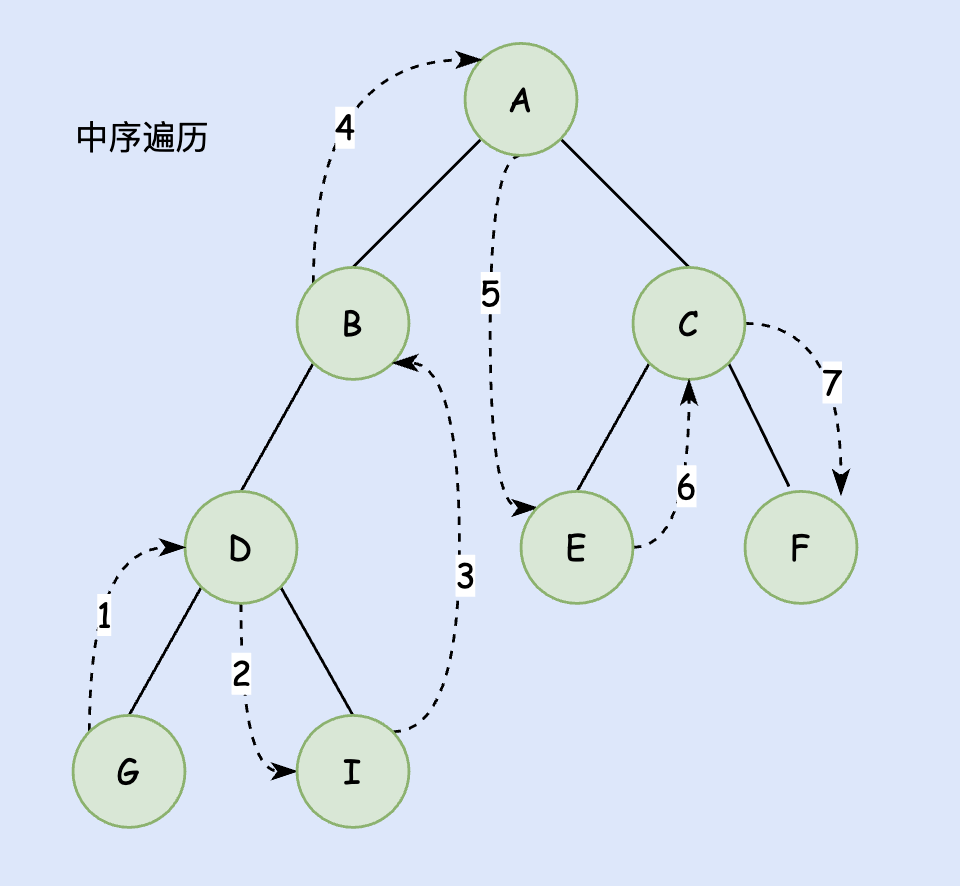
中序遍历

中序遍历的顺序为: Left -> Val -> Right
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
// 递归
func InorderTraversal1(root *TreeNode) []int {
out := make([]int, 0)
var inorder func(*TreeNode, *[]int)
inorder = func(root *TreeNode, out *[]int) {
if root == nil {
return
}
inorder(root.Left, out)
*out = append(*out, root.Val)
inorder(root.Right, out)
}
inorder(root, &out)
return out
}
// 迭代
func InorderTraversal2(root *TreeNode) []int {
out := make([]int, 0)
stack := make([]*TreeNode, 0)
node := root
for node != nil || len(stack) > 0 {
for node != nil {
stack = append(stack, node)
node = node.Left
}
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
out = append(out, node.Val)
node = node.Right
}
return out
}
|
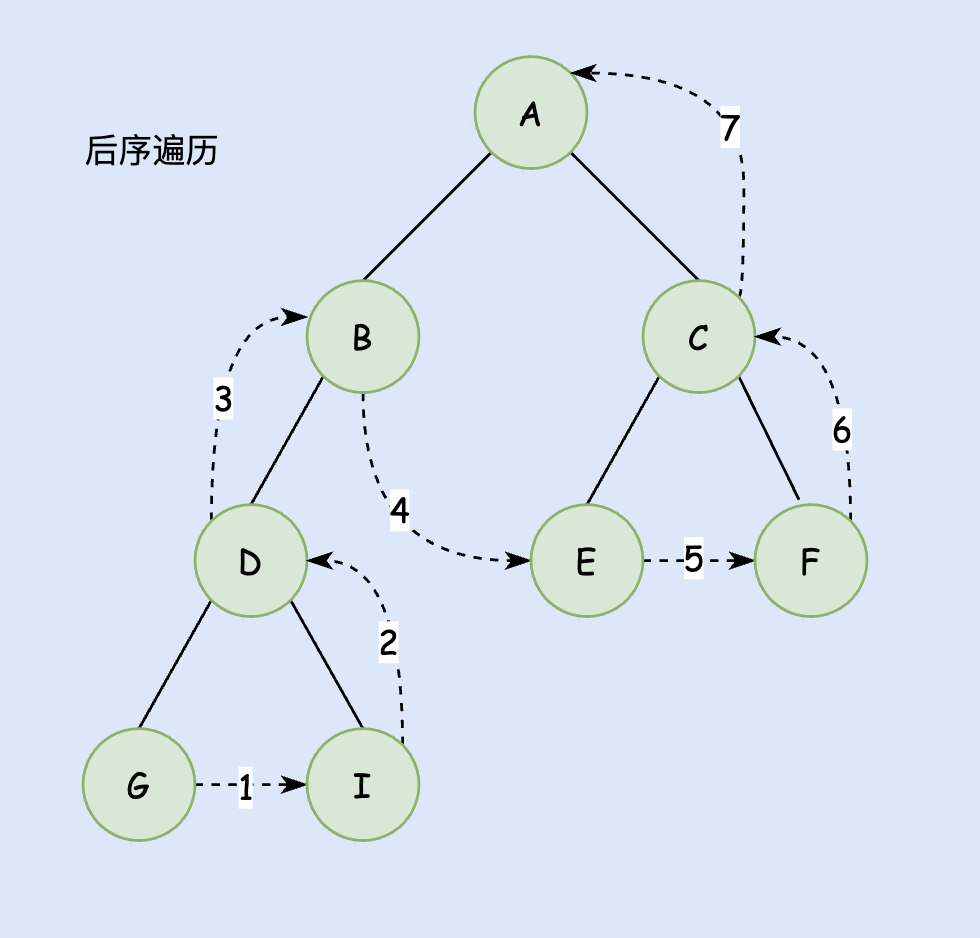
后序遍历

后序遍历的顺序为:Left -> Right -> Val
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
// 递归
func postorderTraversal1(root *TreeNode) []int {
out := make([]int, 0)
var traversal func(*TreeNode, *[]int)
traversal = func(root *TreeNode, out *[]int) {
if root == nil {
return
}
traversal(root.Left, out)
traversal(root.Right, out)
*out = append(*out, root.Val)
}
traversal(root, &out)
return out
}
// 迭代
func postorderTraversal2(root *TreeNode) []int {
out := make([]int, 0)
stack := make([]*TreeNode, 0)
var prev *TreeNode
node := root
for node != nil || len(stack) > 0 {
for node != nil {
stack = append(stack, node)
node = node.Left
}
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
if node.Right == nil || node.Right == prev {
out = append(out, node.Val)
prev = node
node = nil
} else {
stack = append(stack, node)
node = node.Right
}
}
return out
}
|
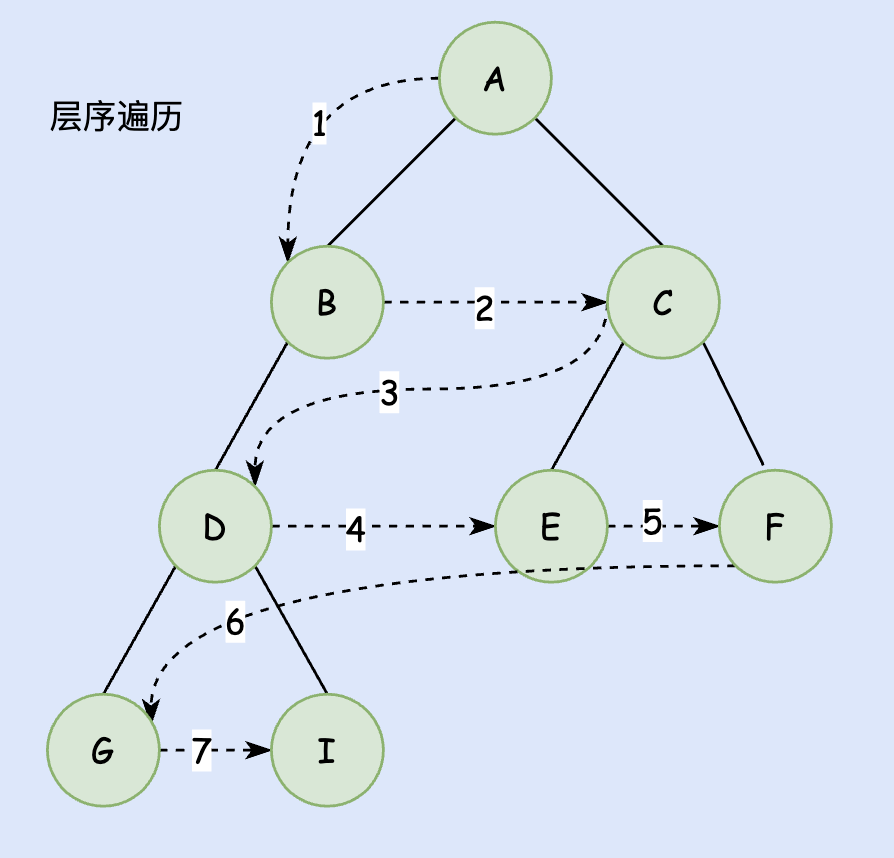
层序遍历

遍历顺序为: Val -> Left -> Right,再逐层进行。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
// 迭代
func levelTraversal(root *TreeNode) []int {
if root == nil {
return []int{}
}
out := make([]int, 0)
node := root
queue := make([]*TreeNode, 0)
queue = append(queue, node)
for len(queue) > 0 {
length := len(queue)
tmp := make([]*TreeNode, 0)
for i := 0; i < length; i++ {
node = queue[i]
out = append(out, node.Val)
if node.Left != nil {
tmp = append(tmp, node.Left)
}
if node.Right != nil {
tmp = append(tmp, node.Right)
}
}
queue = tmp
}
return out
}
|
morris 遍历
二叉树遍历的时间复杂度为 O(n),空间复杂度为 O(n)。但是有一种进阶的遍历方式,可以将空间复杂度优化为 O(1)。它就是 morris 遍历。
morris 遍历的原理是利用的是树的叶节点左右孩子为空(树的大量空闲指针),实现空间开销的极限缩减。
morris 遍历的实现原则
记作当前节点为cur。
- 如果 cur 无左孩子,cur 向右移动( cur = cur.Right)
- 如果 cur 有左孩子,找到 cur 左子树上最右的节点,记为 mostright
- 如果 mostright 的 right 指针指向空,让其指向 cur,cur 向左移动(cur = cur.Left)
- 如果 mostright 的 right 指针指向 cur,让其指向空,cur 向右移动(cur = cur.Right)
实现以上的原则,即实现了morris遍历。
morris 前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
func MorrisPreorderTraversal(root *TreeNode) []int {
vals := make([]int, 0)
var p1, p2 *TreeNode = root, nil
for p1 != nil {
p2 = p1.Left
if p2 != nil {
for p2.Right != nil && p2.Right != p1 {
p2 = p2.Right
}
if p2.Right == nil {
vals = append(vals, p1.Val)
p2.Right = p1
p1 = p1.Left
continue
}
p2.Right = nil
} else {
vals = append(vals, p1.Val)
}
p1 = p1.Right
}
return vals
}
|
morris 中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
func MorrisInorderTraversal3(root *TreeNode) []int {
vals := make([]int, 0)
var p1, p2 *TreeNode = root, nil
for p1 != nil {
p2 = p1.Left
if p2 != nil {
for p2.Right != nil && p2.Right != p1 {
p2 = p2.Right
}
if p2.Right == nil {
p2.Right = p1
p1 = p1.Left
continue
}
vals = append(vals, p1.Val)
p2.Right = nil
p1 = p1.Right
} else {
vals = append(vals, p1.Val)
p1 = p1.Right
}
}
return vals
}
|
morris 后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
func MorrisPostorderTraversal(root *TreeNode) []int {
if root == nil {
return nil
}
cur := root
out := make([]int, 0)
var mostRight *TreeNode
for cur != nil {
mostRight = cur.Left
if mostRight != nil {
for mostRight.Right != nil && mostRight.Right != cur {
mostRight = mostRight.Right
}
if mostRight.Right == nil {
mostRight.Right = cur
cur = cur.Left
continue
} else {
mostRight.Right = nil
printEdge(cur.Left, &out)
}
}
cur = cur.Right
}
printEdge(root, &out)
return out
}
func printEdge(node *TreeNode, out *[]int) {
tail := reverse(node)
cur := tail
for cur != nil {
*out = append(*out, cur.Val)
cur = cur.Right
}
reverse(tail)
}
func reverse(node *TreeNode) *TreeNode {
var pre, next *TreeNode
for node != nil {
next = node.Right
node.Right = pre
pre = node
node = next
}
return pre
}
|
小结
树是一种较复杂的数据结构,本节介绍树的结构、特点和性质,重点介绍二叉树,及其遍历方式。起始还有其他许多特殊的树,因为比较复杂这里就不在赘述。
堆
定义
堆是一种特殊的数据结构,满足以下两个特点:
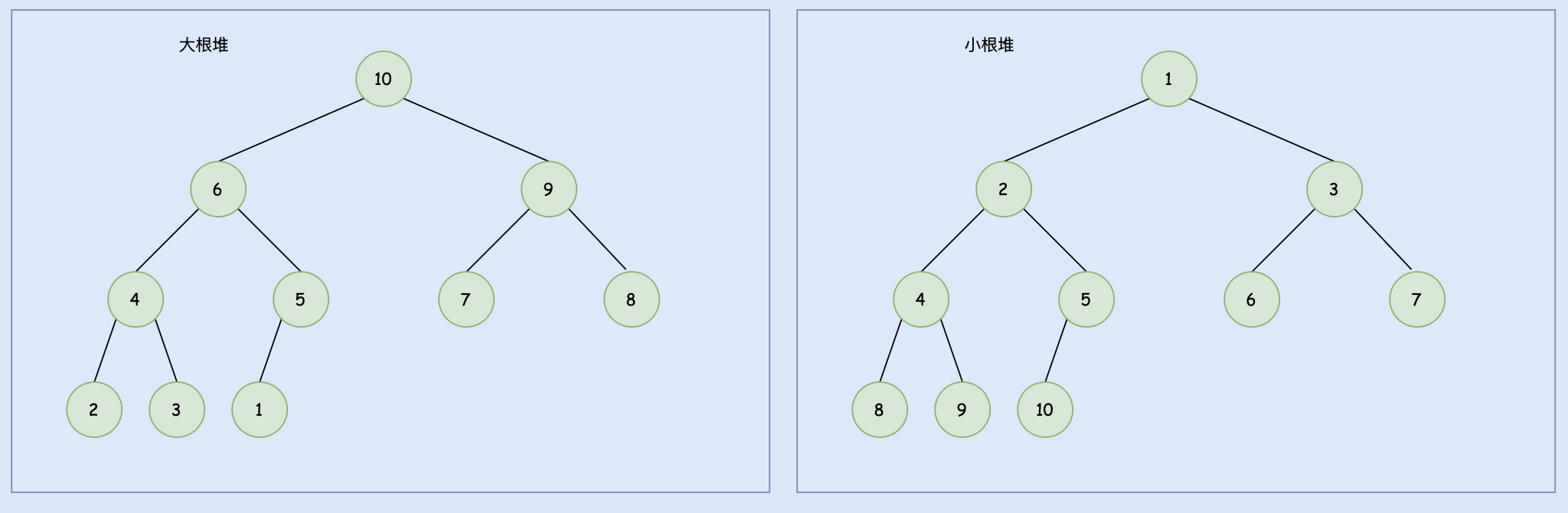
- 它是一棵完全二叉树。
- 每个非叶子结点的子节点要么都小于该节点(大根堆),要么都大于该节点(小跟堆)。
堆分成大根堆和小根堆:

大根堆的根结点为最大值,小根堆的根结点为最小值。
实现
golang 标准库 container/heap 可以用来实现堆。
大根堆代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
type IntHeap []int
func (h IntHeap) Len() int { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }
func (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *IntHeap) Push(x interface{}) {
*h = append(*h, x.(int))
}
func (h *IntHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[:n-1]
return x
}
type MaxHeap struct {
data *IntHeap
}
func NewMaxHeap() *MaxHeap {
data := &IntHeap{}
heap.Init(data)
return &MaxHeap{data: data}
}
func (h *MaxHeap) Push(v int) {
heap.Push(h.data, v)
}
func (h *MaxHeap) Pop() (int, error) {
if h.data.Len() == 0 {
return -1, fmt.Errorf("empty heap")
}
v := heap.Pop(h.data)
return v.(int), nil
}
func (h *MaxHeap) Top() (int, error) {
if h.data.Len() == 0 {
return -1, fmt.Errorf("empty heap")
}
return (*h.data)[0], nil
}
|
小结
堆可以用于实现优先队列和堆排序。
 循环链表的尾指针指向头节点,它可以将尾部插入和删除的时间节点优化为 O(1)。
循环链表的尾指针指向头节点,它可以将尾部插入和删除的时间节点优化为 O(1)。