数据结构和算法是编程的两个核心部分。之前我们介绍了几种常见的数据结构,但是要解决实际的问题光有数据结构还不够,我们还需要知道处理这些数据结构的顺序和方法,也就是算法。
算法是一个很抽象的概念,处理不同的问题可能需要不同的算法或者有好几种不同算法可以处理相同的问题。虽然算法有无数中,但是内在的指导思想是有限的。本篇我们就来了解几种常见的算法思想。
穷举
定义
穷举(也称枚举) 是一种最简单的算法思想。它的核心是将可能的解一一列举出来,然后根据条件进行验证,得到最终所有解。
使用穷举算法解题的基本思路如下:
- 确定穷举对象、穷举范围和判断条件。
- 列举出所有的解,验证每个解是否符合条件。
同时我们也要注意剔除掉许多无效解,避免要验证的可能解过多。
解题
接下来我们使用穷举算法来解 LeetCode-1534 题。

我们根据题目所给出的信息先来确定穷举范围和判断条件。题目要求列举出所有解,所以使用三重遍历选出所有可能的元组。又因为条件 0 <= i < j < k < arr.length,可以缩小 i、j、k 的初始范围。
1
2
3
|
0 <= i < arr.length - 2
i + 1 <= j < arr.length - 1
j + 1 <= k < arr.length
|
在根据条件得出所有解。最终代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
func countGoodTriplets(arr []int, a int, b int, c int) int {
length := len(arr)
count := 0
for i := 0; i < length-2; i++ {
for j := i + 1; j < length-1; j++ {
// 提前退出,避免无效循环
if abs(arr[i]-arr[j]) > a {
continue
}
for k := j + 1; k < length; k++ {
if abs(arr[j]-arr[k]) <= b && abs(arr[i]-arr[k]) <= c {
count += 1
}
}
}
}
return count
}
func abs(n int) int {
if n < 0 {
return -n
}
return n
}
|
该算法的复杂度:
- 时间复杂度:主要是三重循环,时间复杂度为 $O(n^3)$。
- 空间复杂度:使用遍历保存符合元组个个数,因此为 $O(1)$。
递推
定义
递推算法能够通过已知的某个条件,利用特定的关系得出中间推论,然后逐步递推,直到得到结果为止。和穷举不同的是递推每次会记录当前的状态,再计算下次的结果。
递推算法一般分成两种:
- 顺推法:从已知条件出发,逐步推算出要解决问题的方法。例如斐波那契数列就可以通过顺推法不断递推算出新的数据。
- 逆推法:从已知的结果出发,用迭代表达式逐步推算出问题开始的条件,即顺推法的逆过程。
题解
我们使用递推算法来解 leetcode题目

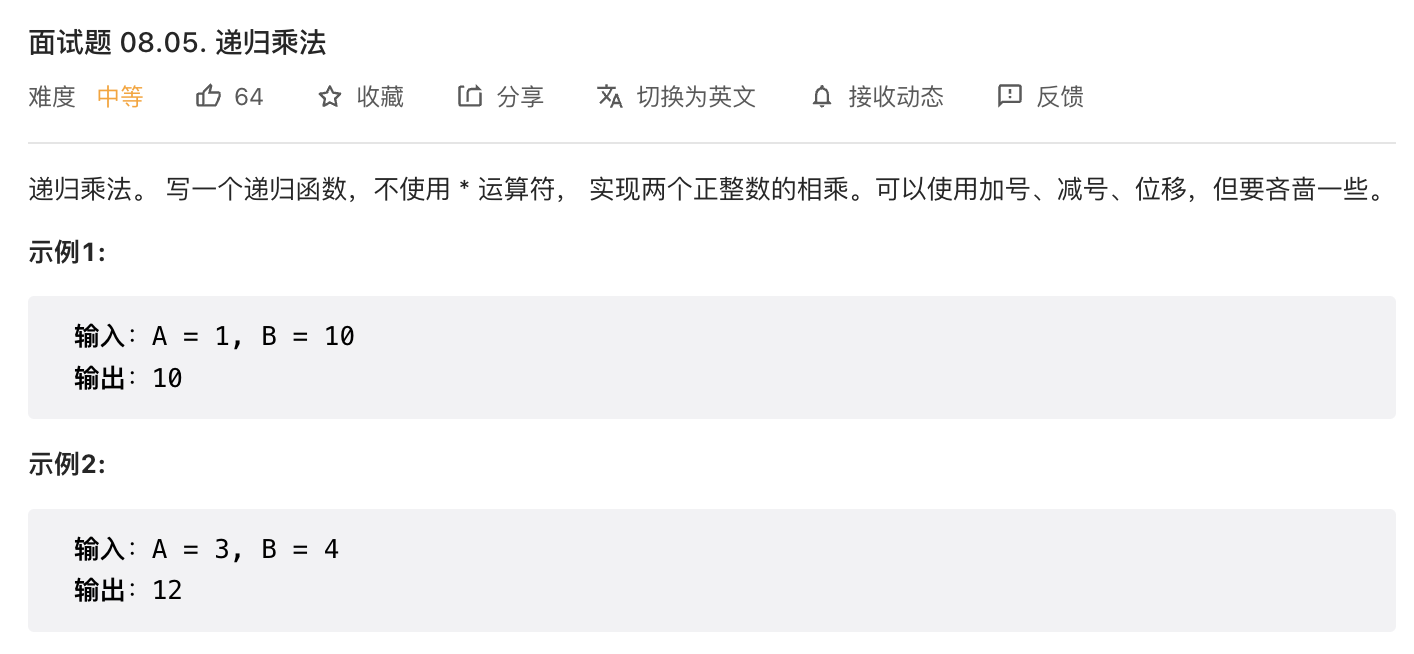
这道提出的要求是使用递归,但是我们也可以使用递推方式来解答。
题目要求计算俩个数的乘积但不能使用乘法符号,那我们可以使用加法来代替乘法。只要循环 B 次,每次累加 A 并保存到和。代码如下。
1
2
3
4
5
6
7
|
func multiply(A int, B int) int {
sum := 0
for i := 0; i < B; i++ {
sum += A
}
return sum
}
|
复杂度分析:
- 时间复杂度:使用一轮循环,因此为 $O(n)$。
- 空间复杂度:结果保存到 sum 变量,因此为 $O(1)$。
递归
定义
递归算法是把问题转化成规模更小的同类子问题,先解决子问题,再通过相同的求解过程逐步解决更高层次的问题,最终获得最终的解。
在实现的过程中,最重要的是确定递归过程终止的条件,也就是迭代过程跳出的条件判断。否则,程序会在自我调用中无限循环,最终导致内存溢出而崩溃。
题解
我们使用递归算法来解 leetcode题目

这道题目要求求是否存在一个整数 x 使得 $n == 2^x$。我们就可以根据这个公式计算 x 的值。递归的结束条件有两种:
- x > n: 表示 n 不是 2 的冥。
- x == n: 表示 n 为 2 的冥。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func isPowerOfTwo(n int) bool {
if n == 1 {
return true
}
return power(n, 1)
}
func power(n, x int) bool {
if x > n {
return false
}
if x == n {
return true
}
return power(n, x * 2)
}
|
复杂度分析:
- 时间复杂度: 递归计算 x 的值,所以为 $O(n)$。
- 空间复杂度: 使用 x 存储 2 的冥,所以为 $O(1)$。
贪心
定义
贪心算法也是将问题分解成多个小问题,但是贪心算法会得出每个步骤的局部最优解,从而得出全局解。
需要注意的是局部的最优解不等于全局最优解,所以当要求取得全局最优解时需要谨慎使用贪心算法。
贪婪法的基本步骤:
- 从某个初始解出发;
- 采用迭代的过程,当可以向目标前进一步时,就根据局部最优策略,得到一部分解,缩小问题规模;
- 将所有解综合起来。
题解
我们使用贪心算法来解 leetcode题目

列表中包含 5、10、20 美元,分三种情况:
- 5 美元时直接收取。
- 10 美元时,如果有剩余的 5 美元,找 5 美元,收取 10 美元。
- 20 美元时,如果有剩余的 10 美元和 5 美化,直接兑换并收取,否则,尝试找 3个 5 美元 (因为 5 美元的用途大于 10 美元)。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
func lemonadeChange(bills []int) bool {
five, ten := 0, 0
for _, b := range bills {
if b == 5 {
five += 1
}
if b == 10 {
if five > 0 {
five -= 1
ten += 1
} else {
return false
}
}
if b == 20 {
if five > 0 && ten > 0 {
five -= 1
ten -= 1
} else if five > 2 {
five -= 3
} else {
return false
}
}
}
return true
}
|
复杂度分析:
- 时间复杂度:遍历列表为 $O(n)$。
- 空间复杂度: 使用两个变量保存收取的零钱,所有为 $O(1)$。
模拟
定义
模拟思想就是对真实场景尽可能的模拟,然后通过计算机强大的计算能力对结果进行预测。
题解
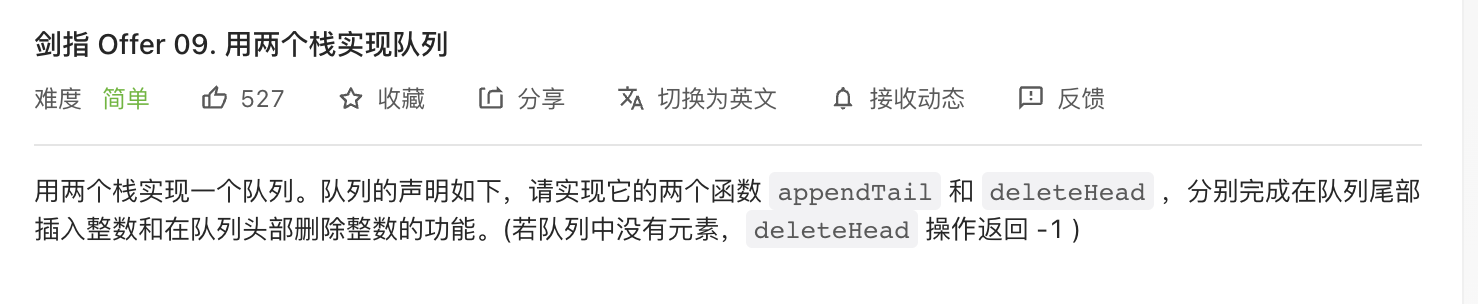
我们使用模拟算法来解 leetcode题目

栈的特点是先进后出,队列的特点是先进先出。直接使用栈肯定不行,我们可以使用两个栈 head、tail,分别对应队列的入队和出队。
元素每次入队时,全部保存到 tail 栈,当元素出队时,先检查 head 是否为空。如果 head 为空,直接将 tail 的值全部放入 head 中。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
type CQueue struct {
head []int
tail []int
}
func Constructor() CQueue {
return CQueue{
head: make([]int, 0),
tail: make([]int, 0),
}
}
func (this *CQueue) AppendTail(value int) {
this.tail = append(this.tail, value)
}
func (this *CQueue) DeleteHead() int {
if len(this.head) > 0 {
v := this.head[len(this.head)-1]
this.head = this.head[:len(this.head)-1]
return v
}
if len(this.tail) > 0 {
for i := len(this.tail) - 1; i >= 0; i-- {
this.head = append(this.head, this.tail[i])
}
this.tail = make([]int, 0)
return this.DeleteHead()
}
return -1
}
|
分治
定义
分治思想,顾名思义就是分而治之。核心步骤为 一分、二治。先将主问题自顶向下分解成更小的细颗粒度子问题,之后就是自底向上将子问题的解合并到主问题中。
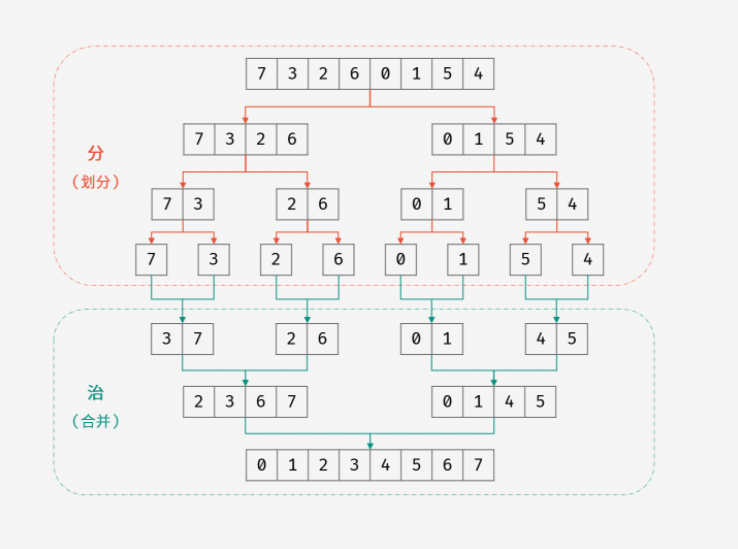
例如排序算法中的归并排序就是典型的分治思想:

将数组拆分为单个元素,再对元素两两排序、合并,不断向上合成,直到排序完成。
题解
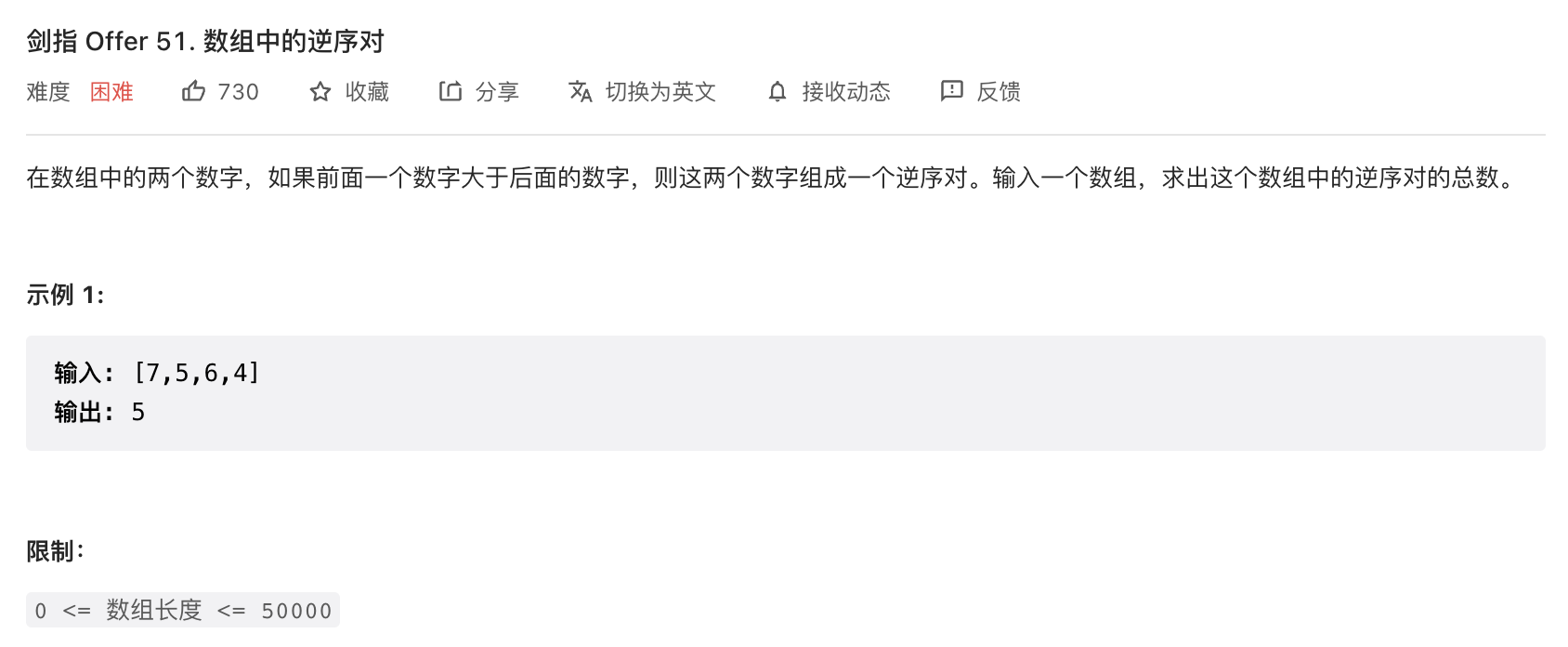
我们使用模拟算法来解 leetcode题目

这道题目可以看作归并排序的变形,每次归并排序时,元素之间需要交互位置时就表示这两个数组组成一个逆序对。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
func reversePairs(nums []int) int {
tmp := make([]int, len(nums))
return mergeSort(0, len(nums)-1, nums, tmp)
}
func mergeSort(l, r int, nums, tmp []int) int {
if l >= r {
return 0
}
m := (l + r) / 2
res := mergeSort(l, m, nums, tmp) + mergeSort(m+1, r, nums, tmp)
i, j := l, m+1
for k := l; k <= r; k++ {
tmp[k] = nums[k]
}
for k := l; k <= r; k++ {
if i == m+1 {
nums[k] = tmp[j]
j += 1
} else if j == r+1 || tmp[i] <= tmp[j] {
nums[k] = tmp[i]
i += 1
} else {
nums[k] = tmp[j]
res += m - i + 1 // 统计逆序对
j += 1
}
}
return res
}
|
复杂度分析:
- 时间复杂度: 使用归并算法,因此时间复杂度为 $O(n \log{n})$。
- 空间复杂度: 使用变量保存排序后的数组,因此为 $O(n)$。
回溯
定义
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种
走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。—— 百度百科
回溯算法有一套固定的模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
res = [] # 定义全局变量保存最终结果
state = [] # 定义状态变量保存当前状态
p,q,r # 定义条件变量(一般条件变量就是题目直接给的参数)
def back(状态,条件1,条件2,……):
if # 不满足合法条件(可以说是剪枝)
return
elif # 状态满足最终要求
res.append(state) # 加入结果
return
# 主要递归过程,一般是带有 循环体 或者 条件体
for # 满足执行条件
if # 满足执行条件
back(状态,条件1,条件2,……)
back(状态,条件1,条件2,……)
return res
|
题解
我们使用模拟算法来解 leetcode题目

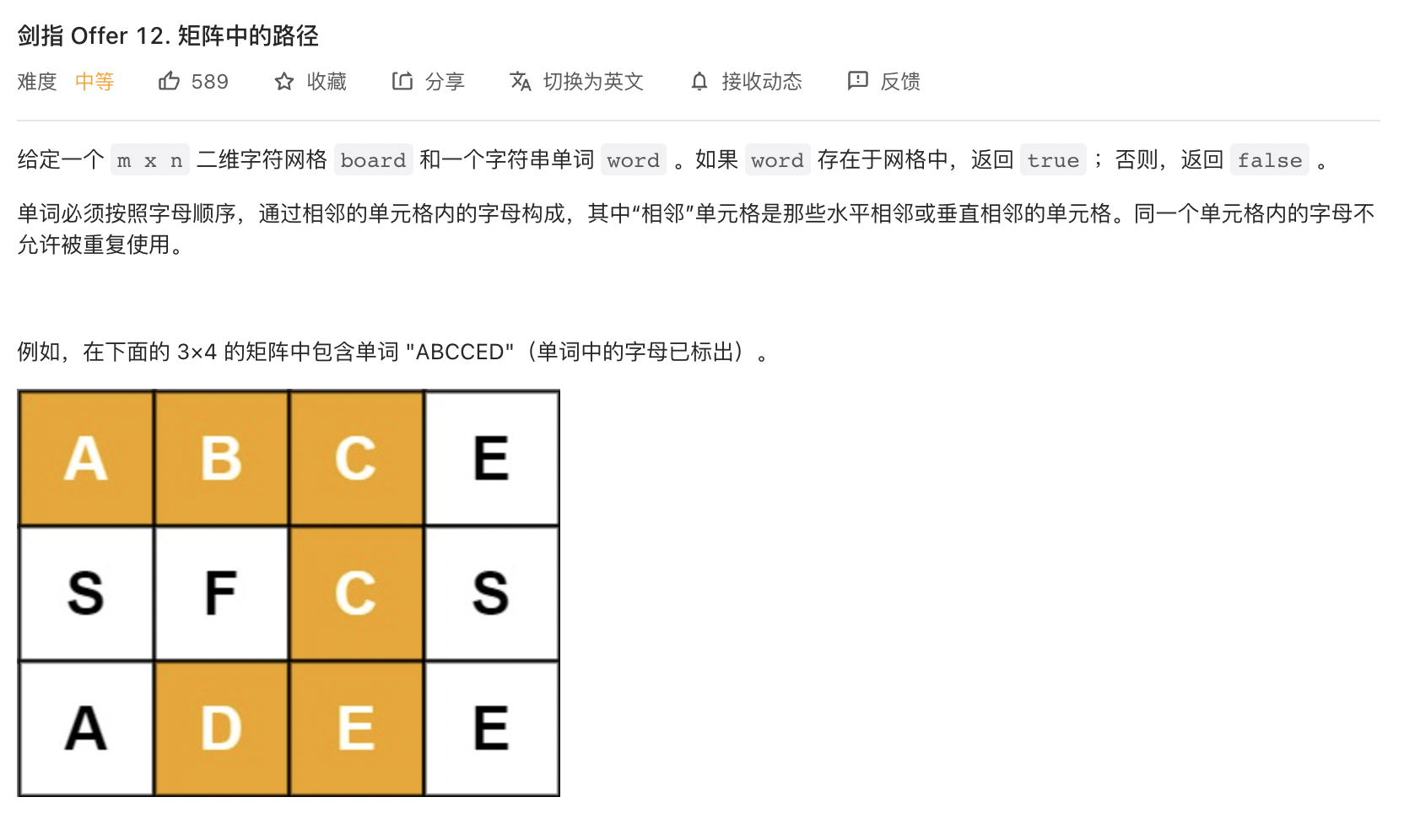
先通过循环确定一个初始点,每次深度遍历前先进行剪枝。 每次经过一个网络时,修改矩阵中元素的值为空,每个网格都可以选择上、下、左、右四个方向的下一个网格。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
func exist(board [][]byte, word string) bool {
for i := 0; i < len(board); i++ {
for j := 0; j < len(board[0]); j++ {
// 确定起始点
if dfs(&board, &word, i, j, 0) {
return true
}
}
}
return false
}
func dfs(board *[][]byte, word *string, i, j, k int) bool {
// 剪枝
if i >= len(*board) || i < 0 || j >= len((*board)[0]) || j < 0 || (*board)[i][j] != (*word)[k] {
return false
}
// 所有路径匹配
if k == len(*word)-1 {
return true
}
// 标记已经走过的网格
(*board)[i][j] = ' '
// 每个网络下一步都有四个方向的选择
boolean := dfs(board, word, i+1, j, k+1) || dfs(board, word, i, j+1, k+1) ||
dfs(board, word, i-1, j, k+1) || dfs(board, word, i, j-1, k+1)
// 状态回溯
(*board)[i][j] = (*word)[k]
return boolean
}
|
复杂度分析:
M,N 分别为矩阵行列大小, KK 为字符串 word 长度。
- 时间复杂度 $O(3^K MN)$ :最差情况下,需要遍历矩阵中长度为 KK 字符串的所有方案,时间复杂度为 $O(3^K)$;矩阵中共有 MN 个起点,时间复杂度为 $O(MN)$ 。
方案数计算: 设字符串长度为 KK ,搜索中每个字符有上、下、左、右四个方向可以选择,舍弃回头(上个字符)的方向,剩下 33 种选择,因此方案数的复杂度为 $O(3^K)$ 。
- 空间复杂度 $O(K)$ : 搜索过程中的递归深度不超过 KK ,因此系统因函数调用累计使用的栈空间占用 $O(K)$。最坏情况下 $K = M$,递归深度为 $MN$ ,此时系统栈使用 $O(MN)$O 的额外空间。
动态规划
定义
动态规划需要将问题划分为多个子问题,但是子问题之间往往不是互相独立的。当前子问题的解可看作是前多个阶段问题的完整总结。
因此这就需要在在子问题求解的过程中进行多阶段的决策,同时当前阶段之前的决策都能够构成一种最优的子结构。这就是所谓的最优化原理。
最优化原理,一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。
同时,这样的最优策略是针对有已作出决策的总结,对后来的决策没有直接影响,只能借用目前最优策略的状态数据。这也被称之为无后效性。
动态规划,简单讲就是利用历史记录,来避免我们的重复计算。而这些历史记录,通常是用一维数组或者二维数组来保存。
动态规划的主要步骤:
- 定义数组元素的含义,设置 dp 记录历史数据。
- 找出数组元素之间的关系式,确定状态转移方程式。
- 找出初始值。
题解
我们使用模拟算法来解 leetcode题目

代入步骤来解答此题。
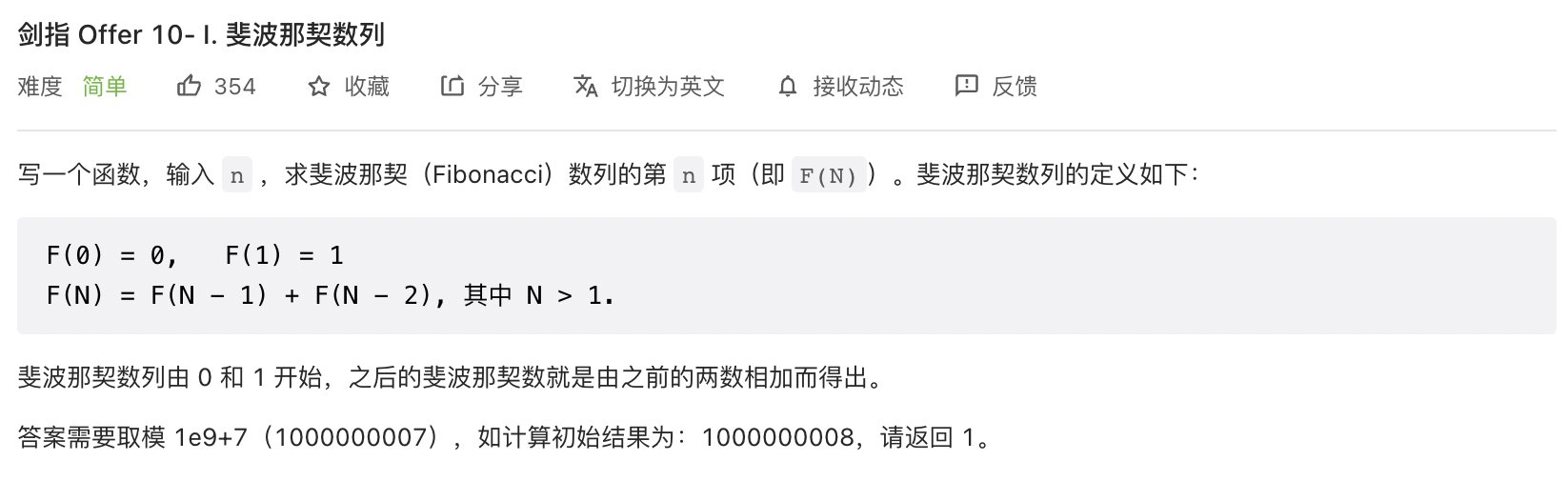
- 使用一维数组 dp[n] 来保存每次计算的斐波那契值。
- 根据斐波那契的定义可得状态转移方程式: $F(i) = F(i-1) + F(i-2)$。
- 确定初始化,F(0) = 0, F(0) = 1。
需要注意的是 n 的最大值为 100,计算结果会超出 int 范围,所以结果取模。
最终代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func fib(n int) int {
if n == 0 {
return 0
}
if n == 1 {
return 1
}
mod := 1e9 + 7
dp := make([]int, n+1)
dp[0], dp[1] = 0, 1
for i := 2; i <= n; i++ {
dp[i] = (dp[i-1] + dp[i-2]) % int(mod)
}
return dp[n]
}
|
复杂度分析:
- 时间复杂度:主要在于循环的时间花费,因此为 $O(n)$。
- 空间复杂度: 使用一维数组 dp 保留每次计算的结果,所以为 $O(n)$,实际可以只使用两个变量保存前两个结果,这样空间复杂度可以优化为 $O(1)$。